We use Snell's equation
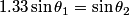 where 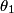 is the angle the the light makes with the normal below the surface of the water and is the angle the the light makes with the normal below the surface of the water and 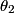 is the angle that the light makes with the normal above the water. The maximum value of is the angle that the light makes with the normal above the water. The maximum value of 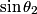 is is 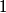 , so total internal reflection occurs when , so total internal reflection occurs when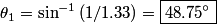 Therefore, answer (C) is correct. |